Lists

#The need for a list

Averaging the price of items in our shopping cart:

; average-2-price: (Number Number -> Number)
; produce the average price of the 2 given items
(define (average-2-price item1 item2)
    (/ (+ item1 item2) 2))

Why is this average-2-price code not flexible? Because when we want to handle more item prices, we have to:

1. Write a new function: average-{N}-price
2. Change the purpose
3. Change the number of parameters the function takes
4. Change the code of the function

; average-3-price: (Number Number Number -> Number)
; produce the average price of the 3 given items
(define (average-3-price item1 item2 item3)
    (/ (+ item1 item2 item3) 3))

; we'd have to create a new function to handle more data?!
; 4
; 5
; ... it gets worse as we add more. It's not sustainable!
; Imagine a 20-100 argument function...
; I wish there was a datatype that can store multiple values

BUT WAIT! Structs can store multiple values in 1 type/variable, so let’s try that!

(define-struct cart [item1 item2])
; Cart is (make-cart Number Number)
; interp. each item{n} is its price

; average-cart-price: (Cart -> Number)
; produces the average price of all the items cart holds
(define (average-cart-price ct)
    (/ (+ (cart-item1 ct)
          (cart-item2 ct)) 2))

(define my-cart (make-cart 9 3))
(average-cart-price my-cart)

We’re getting there! Because the items are now contained within a (make-cart) structure, here’s what we have to change to accomdate for 3 items:

1. The data definition
2. The function code

Contrast this to when functions were just taking the item prices as arguments individually, we no longer have to write a new function or adjust the number of parameters we take in when we want to process more items, we instead change the data definition cart.

Even though structs can hold multiple pieces of data, we still run into the same problem, and that is our cart structure is fixed sized. It can/must only hold the amount of items we tell it to ahead of time as specificed by the amount of fields: item{n}! This which is not realistic! In the real world, when you go shopping, you don’t know the amount of items you want to buy, you often figure it out along the way. In other words, it can be arbitrarily long. The amount of items in a shopping cart can also fluctate between 5-20 as people put things in and out of their shopping cart all the time! If only there was a type of data that is more flexible that grows and shrinks on demand. Drumroll, that’s what lists are for! We’ll learn how to design code such that the data & function definition won’t need to change, just the data itself, e.g (make-cart 9 2 3 4).

Consider our ripple program in 8.07. How many times does the user click? They can click whenever they want, so it’s completely arbitrary! We’ll later expand our ripple program to handle an infinite amount of ripples, and lists will give us the power to do that.

#What is a list?

A list is a compound value datatype that can grow & shrink on demand. BSL treats a list as a single value that can can contain other values inside itself. Imagine a shopping list, you write “milk, eggs, cheese” on a piece of paper, then fold up the paper and put it in your pocket. While it’s folded up, you can think of the list as a single entity. It’s only later, at the store, where you need to go “into” the list and retrieve the individual pieces of information it contains.

;empty and '() are exactly the same, you can imagine (define empty '())
empty
'()
; imagine '() empty, being an empty piece of paper. A list must exist ON something

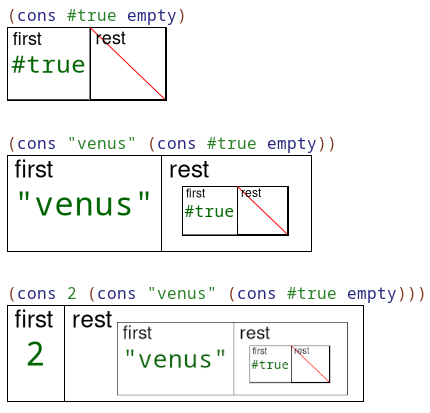
; cons: (Any List -> List)
; short for "construct", cons produces a list

; 1 element list: put #false in FRONT of the empty list
(define stuff (cons #false empty))
(define grocceries (cons "eggs" (cons "chips" empty)))
(define numbers-ls (cons 4 (cons 3 (cons 6 empty))))
(define whatever-ls (cons 9 (cons #true (cons "asdf" empty))))
; silly evaluation:
(define op (cons (* 2 4) (cons 3 (cons (string-append "asd" "qw") empty))))

; first: (ListOfAny -> Any)
; produces the first value of the given list (assuming a non-empty list)
(first stuff) ; produces #false
(first grocceries) ; produces "eggs"
(first numbers-ls) ; produces 4

; rest: (ListOfAny -> ListOfAny)
; produces a list with the first element excluded of a non-empty list
(rest stuff) ; produces the empty list
(rest grocceries) ; produces (cons "chips" empty)
(rest numbers-ls) ; produces (cons 3 (cons 6 empty))

; how do you get the 2nd element of a list? Get me "chips" from grocceries
(first (rest numbers-ls))
; what happens if we try to get the 2nd element of a 1 long list?

; how do you get the 3rd element of a list? Get me 6 in the numbers-ls
(first (rest (rest numbers-ls)))
; what happens if we try to get the 3rd element of a 2 long list

; empty?: (Any -> Boolean)
; produces #true if given an empty, #false otherwise
(empty? 123) ; produces #false
(empty? grocceries) ; produces #false
(empty? empty) ; produces #true

; cons?: (Any -> Boolean)
; Determines whether some value is a constructed list. (do not confuse with "cons". 1 letter difference)
(cons? 123) ; #false
(cons? "asdff") ; #false
(cons? empty) ; #false
(cons? (cons 99 empty)) ; #true
(cons? (cons "moo" (cons "peck" empty))) ; #true

; list? (Any -> Boolean)
; produces #true if given an kind of list(empty or cons)
(list? "asdf") ;#false
(list? #true) ;#false
(list? 21) ;#false
(list? (cons 3 empty)) ;#true
(list? empty) ;#true

The List data definition

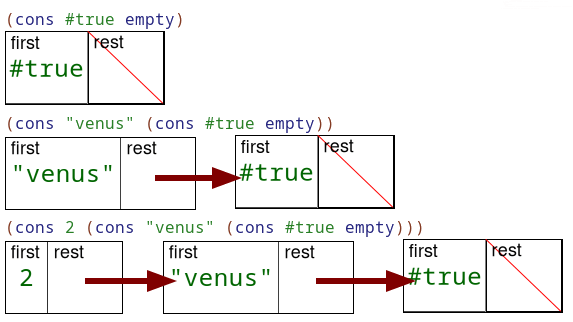
Let’s review cons and lists in a little more detail because it looks a bit weird.

; A List is one of:
; - empty
; - (cons Any List)
; interp. represents a list of Any type of data, e.g an arbitrarily long sequence

; cons: (Any List -> List)
; short for "construct", cons produces a list

(define stuff (cons #false empty))
(define grocceries (cons "eggs" (cons "chips" empty)))
(define numbers-ls (cons 4 (cons 3 (cons 6 empty))))

The List data definition has a self reference, and its why we see this nesting of cons. It’s easy to miss that the 2nd argument must be a list, because the data definition is a comment that is easily glanced over. One of the #1 mistakes people make is not obeying the signature, and not having good data definitions that describe what things are. It has to be a list, either the empty '() list, or another cons list. All lists must eventually end with the empty list. It may take a few reads to interalize what data definitions are saying about lists.

Here are some examples of syntactically invalid lists, try and spot the problem and fix them in your editor

(define bag (cons "choclate" (cons "tomato") empty))
(define nums (cons 3 2))

You must type lists out in a cons chain sort of way for now to get used to the structure of them, but in the future, there’s going to be a much easier way.

#Nested Diagram

#Box and Pointer Diagram

Box and pointer diagrams are much more common as they take up less space and are easier to follow as the amount of items increases.

#List basics quiz

(define L1 (cons "James" (cons "Alice" (cons "Bob" empty))))
(define L2 (cons 1 empty))

(define L1 (cons "James" (cons "Alice" (cons "Bob" empty))))
(define L2 (cons 1 empty))

(define L1 (cons "James" (cons "Alice" (cons "Bob" empty))))
(define L2 (cons 1 empty))

(define L1 (cons "James" (cons "Alice" (cons "Bob" empty))))
(define L2 (cons 1 empty))

(first (cons (cons 99 empty) (cons 45 empty)))

(define x (cons (cons 99 empty) (cons 45 empty)))

(cons (cons 4 empty) (cons 3 empty))

; swap: (ListOfAny -> ListOfAny)
; consumes a two element list and swaps their order
(check-expect
    (swap (cons 3 (cons 2 empty)))
          (cons 2 (cons 3 empty)))

(check-expect
    (swap (cons 0 (cons 5 empty)))
          (cons 5 (cons 0 empty)))

; (define (swap ls) empty)

(define (swap ls)
    (... ls))

(define (swap ls)
    (cons (first (rest ls))
        (cons (first ls) empty)))

Lists are where things start ramping up in difficulty as you’ll see shortly, so it’s very important you have an intuitive grasp of these basic list operations!

Extra: Internals

This is an extra section if you want to know the “internals” of lists.
There is a clever trick that we can define structures such that we can chain values together. What we do is that in our data definition, we do a self reference. The empty is just a distinct type, empty-link

; Link is one of:
; - (make-empty-Link)
; - (make-link Any Link)

(define-struct empty-link []) ; has no fields
(define-struct link [first rest])
; (link-first Link) = "first"
; (link-rest Link) = "rest"

(make-empty-link) ; equiv to: empty or '()
(make-link 8 (make-empty-link)) ; 1 element list

(make-link 8
    (make-link 2 (make-empty-link))) ; 2 element list

; link-temp : (Link -> ???)
(define (link-temp lnk)
  (cond
    [(empty-link? lnk) ...]
    [else
     (... (link-first lnk)
          (link-temp (link-rest lnk)))]))

Natural Numbers as recursive types

; Natural is one of:
; - 0
; - (add1 Natural)

(define two (add1 (add1 0)))

; natural-temp : (Natural -> ???)
(define (natural-temp n)
  (cond
    [(= 0 n) ...]
    [else
     (... n (natural-temp (sub1 n)))])) ;sub1 can be thought of as "rest"

Trees

; An FamilyTree(FT) is one of:
; - #false
; - (make-person String Number String FamilyTree FamilyTree)
; interp. #false means no parent

(define-struct person [name birth-year eyes mother father])
; Person is (make-person String Number String FamilyTree FamilyTree)