What is Generative Recursion aka Algorithms?

Although most of the functions programmers write will be structurally recursive, that is that the function template will just fall out of the data definition:

; A ListOfNumber is one of:
; - empty
; - (cons Number ListOfNumber) ; first and rest

(define (list-num-temp lst)
  (cond
    [(empty? lst) ...]
    [else
     (... (first lst) ; Number
          ; recursive call is straight from the data def
          (list-num-temp (rest lst)))]))

Generative recursion is where the recursive call is less based on the structure of the data, and more from the problems domain knowledge. It could draw upon descriptions of math formulas, fractals, real life algorithms, and many more. It could require you to rearrange the problem, solve several related sub problems, and then combining them together before you do the recursive call. They often vary but they look somewhat like this:

(define (gen-rec-fn p)
  (cond
    [(trivial? p) (solve p)]
    [else
     (combine-solutions
       p
       (gen-rec-fn
         (sub-problem p)))]))

You will still have a base case, you will still have a recursive call, it’s just that it isn’t always going to be so obvious compared to structural recursion. You won’t always have your base case checking for empty, or have your recursive call on (rest lst). You’ll have to derive that from elaborating and coming up with the extra insight, the AHA moment, yourself.

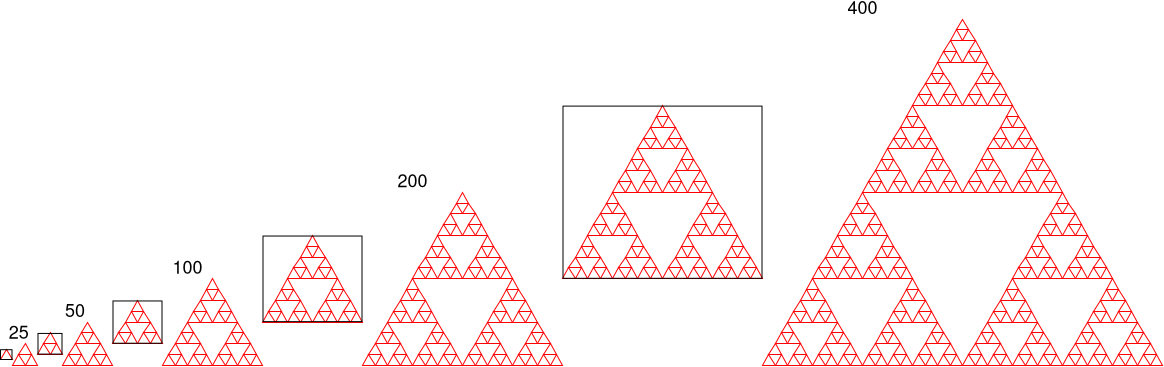
#Fractals

#Fractals step by step animation

; s-triangle : (Number -> Image)
(define (s-triangle side) empty-image)

Now we need to answer the questions of generative recursion.

What is the trival case?

The trival case is what happens if we are given a side lengh that is too small? Well then we should have a base case that is the smallest triangle.

How do we combine the results of the trival case and potential sub problems to solve the overarching problem? Aka, the generative case!

Since the base case gives us a triangle back, we need to put one triangle beside it, and then one above it to make the 3 stack triangle.

How does it terminate?

The given number(side-length) is getting / 2 at every step, therefore shrinking towards the LIMIT.

We start off wanting to draw a big fractal but the smaller ones have to be drawn first and then used in the building of the bigger one. I recommended you use the stepper to understand how s-triangle mechanically works.

The book How to Design Programs Book(spoilers)‘s has a detailed guide on deconstructing this fractal.